数据表示和存储
定点数和浮点数
- 计算机中只能通过约定小数点的位置来表示
- 定点数——小数点位置约定在固定位置的数
- 浮点数——小数点位置约定为可浮动的数
- 定点小数用来表示浮点数的尾数部分
- 定点整数用来表示整数 分为带符号整数和无符号整数
- 任何实数:$X=(-1)^S \times M \times R^E$ S表示正负;M为二进制定点小数,称为X的尾数;E是二进制定点整数,称为X的阶或指数;R是基数,可以为2、4、16等。只要表示S、M和E三个信息就能确定X的值,这称为浮点数。
定点数的编码表示
- 定点数的编码
- 原码、补码、移码、反码(很少用)
-
原码:正号0 负号1 其余二进制表示
-
缺点:
- 0的表示不唯一,不利于编程
- 加减运算方式不同意
- 需要额外对符号位进行处理,不利于硬件设计
- 当a<b 实现a-b比较困难
从50年代开始,整数都采用补码表示,但浮点数的尾数用原码定点小数表示
-
-
移码:将每一个数值加上一个偏置常数(Excess / Bias)
-
通常当编码位数为n时,bias取$2^{n-1} 或2^{n-1}-1(如IEEE 754)$
- Ex. n=4: $E_{biased} = E+2^3 (bias=2^3=1000B)$
- -8(+8) ~ 0000B
- -7(+8) ~ 0001B
- …..
- 0(+8) ~ 1000B
- …..
- +7(+8) ~ 1111B
- Ex. n=4: $E_{biased} = E+2^3 (bias=2^3=1000B)$
-
用移码来表示指数(阶码)便于浮点数加减运算时的对阶操作(比较大小)
- Ex: $1.01\times 2 ^{-1}+1.11\times2 ^3$ $1.01\times2 ^{-1+4}+1.11\times2 ^{3+4}$
- 补码:111(-1)<011(3)? 移码:011(3)<111(7)
- Ex: $1.01\times 2 ^{-1}+1.11\times2 ^3$ $1.01\times2 ^{-1+4}+1.11\times2 ^{3+4}$
-
-
补码:模运算 在一个模运算系统中,一个数与它除以“模”后的余数等价。
$10-4=6$
$10+8=18\equiv6 (mod 12)$
$10-4\equiv10+8 (mod 12)$
$-4\equiv8 (mod 12)$
$结论1:一个负数的补码等于模减该负数的绝对值$
$结论2:对于某一确定的模,某数减去小于模的另一数,总可以用该数加上另一数负数的补码来代替(在模运算中减法和加法可以转换)$
$Ex. 9828-1928=9828+(10^4-1928)$
$=9828+8072$
$=17900$
$=7900(mod 10^4)$

$[X]_补=2 ^n+X (-2 ^n<=X<2 ^n,mod 2 ^n)$ X是真值 $[X]_补$是机器数
$[-2 ^{n-1}]_补=2 ^n-2 ^{n-1}=10…0(n-1个0)$
$[-1]_补=2 ^n-0…01=11…1(n个1)$
$[+0]_补=[-0]_补=00…0(n个0)$
$[-01111011]_补=2 ^8-01111011=100000000-01111011=11111111-01111011+1=10000100+1=10000101=85H$
负数求补码 简便方法:从右向左遇到的第一个1的前面各位取反
变形补码:表示溢出(两位不同则为溢出) 8->1000(补码)->01000(变形补码)
求补码的真值:符号位0 数值部分相同;符号位1 负数,数值位取反 末尾加1
C语言中的整数
无符号整数(Unsigned integer)
-
LSB(least significant bit)最低有效位 MSB最高有效位
-
一般在结果没有负值的场合用无符号数:地址运算,编号表示等等
带符号整数(Signed integer)
-
有三种编码表示
- 原码:定点小数,用来表示浮点数的尾部
- 移码:定点整数,用于表示浮点数的阶(指数)
- 补码:50年代以来 所有计算机都用补码来表示带负号整数
-
为什么用补码表示带符号整数?
- 补码运算系统是模运算系统,加减统一
- 数0的表示唯一,方便使用
- 比原码多表示一个最小负数
若同时有无符号和带符号整数,则C编译器将带符号整数强制转换为无符号数
| 范围 | C90类型 |
|---|---|
| 0~$2 ^{31}-1$ | int |
| $2 ^{31}$~$2 ^{32}-1$ | unsigned int |
| $2 ^{32}$~$2 ^{63}-1$ | long long |
| $2 ^{63}$~$2 ^{64}-1$ | unsigned long long |
| 范围 | C99类型 |
|---|---|
| 0~$2 ^{31}-1$ | int |
| $2 ^{31}$~$2 ^{63}-1$ | long long |
| $2 ^{63}$~$2 ^{64}-1$ | unsigned long long |
浮点数的编码表示

| 0 | 1-8 | 9-31 |
|---|---|---|
| S | 阶码E | 尾数M |
第0位树符S;第1~8位位8位移码表示解码E(偏置常数为128);第9~31位位24位二进制原码小数表示的尾数M。规格化尾数的小数点后第一位总是1,所以第一位默认1不明显表示出来。这样可用23个数位表示24位尾数。
最大正数:0.11…1 x $2 ^{11…1}$=(1-$2 ^{-24}$) x $2 ^{127}$
最小正数:0.10…0 x $2 ^{00…0}$=(1/2) x $2 ^{-128}$
不同机器浮点数表示不同,所以出现了IEEE 754
IEEE 754标准
Exponent(阶码):
- SP规格化解码范围为0000 0001(-126) ~ 1111 1110(127)
- bias为127(single),1023(double)
Significand(尾数):
- 规格化尾数最高位总是1,所以隐含表示,省1位
- 1+23 bits(single), 1+52 bits(double)
SP: $(-1) ^S \times (1+Significand) \times x ^{Exponent-127}$
DP: $(-1) ^S \times (1+Significand) \times x ^{Exponent-1023}$
例:float型变量x的机器数为BEE00000H,求x的值?
1011 1110 1110 0000 0000 0000 0000 0000
-
数符:1(负数)
-
阶(指数):
- 阶码:0111 1101 B = 125
- 阶码的值:125-127 = -2
-
尾数数值部分:
$1+1\times x ^{-1}+1 \times 2 ^{-2}+0 \times 2 ^{-3}+0 \times 2 ^{-4}…..$
=$1+2 ^{-1}+2 ^{-2}=1+0.5+0.25=1.75$
-
真值=$1.75 \times 2 ^{-2}=-0.4375$
例:float变量x值为-12.75,求x的机器数是多少?
-12.75=-1100.11B=-1.10011B x $2 ^{3}$
因此,符号S=1
阶码E=127+3=128+2=1000 0010
显式表示的部分尾数Significant=100 1100 0000 0000 0000 0000
x机器数表示为:
1100 0001 0100 1100 0000 0000 0000 0000
转换为十六进制表示为:C14C0000H
规格化数
特殊数
| 0的机器数 | 无穷数 | 非数 | |
|---|---|---|---|
| 阶码 | 全零 | 255(11111111B) | 255 |
| 尾数 | 全零 | 全零 | nonzero |
非规格化数
$(-1) ^S \times 0.XXXXX \times 2^ {-126}$
非数值数据的编码表示
ASCII
0-30H
1-31H
A-41H
a-61H
汉字
输入码:对汉字用相应案件进行编码表示,用于输入
内码:用于再系统中进行存储、查找、传送等处理
字模点阵或轮廓描述:描述汉字字模点阵或轮廓,用于显示、打印
GB2312:94行94列,行号是区号,列位是位号,各为7位
区、位码上各加32(20H
得到两个字节编码 首位设为1,得到内码,避免与ASCII混淆
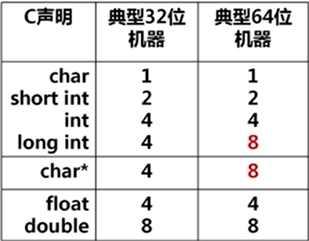
数据宽度和存储量的单位
位bit 字节byte( 现代计算机 存储器按字节编址 字节是最小可寻址单位)
字(word) IA-32中 字 为16位 DWORD(双字 32位) QWORD(64位)
数据存储时的字节排序
大端——数据高位在地址低位——photoshop,JPEG,MacPaint
小端——数据低位在地址地位——GIF,PC Panintbrush,MS RTF
个人总结
- 正数的原码 反码 补码 全都相等(因为反码补码都是为了解决减法引入的)
- 负数 原码符号位为1其余一样 反码是原码取反 补码=反码+1
- 计算机内部计算是用补码计算
四、 乘除运算及浮点数运算
整数乘法运算
当n=4时 5的平方=-7 n为位数
在计算机内部,一个整数x的平方可能是负数,这是因为在计算机中其结果取的是x*x的低n位乘积而高n位中的有效数位被丢弃而造成的。
当 (!x || z/x==y) 为真时【x=0或者z除回去还成立】 z正确;当 $-2^{n-1} <= x*y < 2^{n-1}$ 时(就是不溢出时 当前位数能存 当然不会变),即:乘积的高n位为全0或全1,并等于低n位的最高位,即:乘积的高n+1位为全0或全1
如果是无符号数,只要判断乘积高n位是否全为0就能判断是否溢出
无符号加减运算和带符号加减运算是一样的
无符号乘法与带符号乘法低n位结果一样 高n位不一样(如果采取一样的指令 编译器就无法判断溢出了)(乘法指令不生产溢出标志,编译器可使用2n位成绩来判断是否溢出 PS:DX和AX的关系)
溢出漏洞:申请的数据溢出了,但是计数还是很大,覆盖很大的空间。
